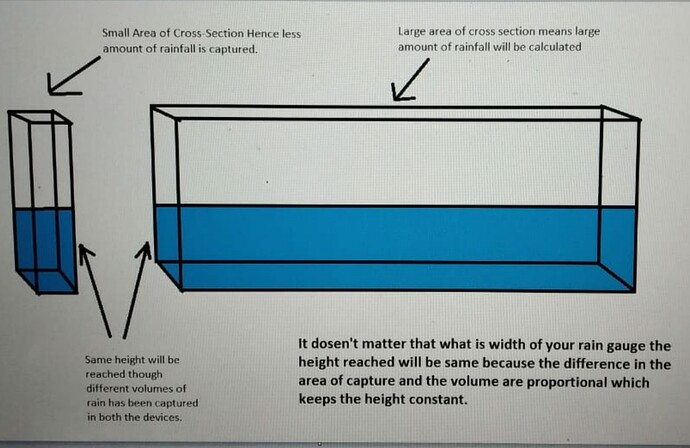
Yesterday @arunan sir suggested a problem with the way rain gauge measure rain. Since water takes the shape of it’s container the rainfall height that we measure must also vary if gauge size is varied. Which is a problem when we compare rainfall by the height of water collected in rain gauge.
2 Likes
This problem though seems is not an issue due to the fact that the change in the dimensions of the rain gauge will also affect the volume of rainfall collected hence keeping the height same.
2 Likes
Is it a height problem or volume problem?
Why not measure in volume?
If volume is measured and height constant, volume filled per unit time will vary.
Dont we have to calculate the amount of rainfall?
how can amount of rainfall be represented in height?
2 Likes
It is the problem of height difference that we thought might occur due to the different volumes of rain gauges
Now to get a unit amount of rainfall and its severity you want to measure the rainfall per unit area.
Which is :
VOLUME of Rainfall / AREA of Land = cm^3/cm^2 = cm [ Dimensional analysis leaves us with length as unit for rainfall per unit area]
So due to that we measure rainfall in height
2 Likes
Not clear, it will be good if you create a demo. And demonstrate about this problem, and also make a video of it and share… @pratittodkar
2 Likes
No size of the rain gauge will not affect your results as far as the size of the mouth of gauge is same as the circumference of the rain gauge. So don’t worry in selecting even a bucket for rain gauge. It should have even circumference through out the gauge.
Tip:- if you are taking a bottle with bottom which in not round, you can pour water upto level where you get even circumference. Then make a mark on that level and measure from that point. 
1 Like
I will try doing a demonstration and filming it.
As an example of my point you can check that in the above mathematical proof I assumed that there is 30 ml (VOLUME)/cm^2 (AREA) and the end results gave the same magnitude though it was in term of HEIGHT.
I got H = 29.999 ( Due to decimal point approximations there was an error of 0.1 )
Whereas (VOLUME) / (AREA) was assumed to 30 ml/ cm^2
1 Like