Bending Light
We discussed the concept of reflection and refraction from the scratch via PhET simulation in the Part I . We will extend our discussion here. ![]()
Here our main focus is the concept of total internal reflection, critical angle and its dependence on the refractive indices of the two medium.
- Link of the event post: click here
- Link of the simulation: https://phet.colorado.edu/en/simulation/bending-light
- Link of the recording: click here
Reflection
- What are the conditions responsible for total internal reflection?
- What is critical angle?
- How to determine the critical angle of a medium if its refractive index is known and vice versa?
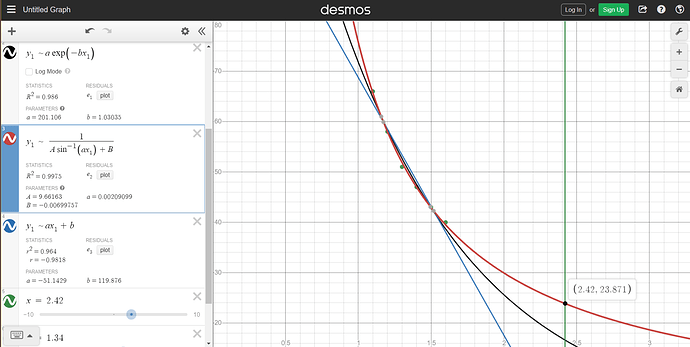
P.S.: So we plotted a graph between the critical angle in degree (y axis) and refractive index (x axis) obtained from simulation using Desmos graphing calculator and then try to estimate the critical angle for diamond using its refractive index by finding a best fit and extrapolating the curve.
We obtained the value of 23.871 degrees which is very close to the actual value.
- Share your thoughts, questions and comments regarding the simulation and your experience during exploring the simulation.
We welcome all kind of suggestions and feedback if this was useful and how can be collectively make it better.
Acknowledgements
Discussion
Collaborators in video resource creation: Deepak Arora, Ravi Sinha, Swarnava Mitra
Credits
-
PhET Interactive Simulations
University of Colorado Boulder
https://phet.colorado.edu -
Desmos Graphing Calculator
Desmos | Graphing Calculator